2023-01-19
Measure for Measure Part II: Length and the Metre
Can we finally stop redefining the way we measure length?
After time comes length; a quality most physical objects have, making it easy to observe and very simple to estimate. Though, nature likes to make exactness difficult. A naturally occurring entity which always possesses the same length is nonexistent — there’s always some variation and it’s usually Gaussian, not too handy when you’re trying to define a consistent and reproducible unit of measure. The solution to this throughout most of history was to simply pick a body part, coin a not so creative name i.e., foot, and hope for the best. But slowly, as science advanced, so too did the accuracy and precision of the measurements involved; a feat made only possible by the scholars who risked their lives through war and revolution to establish a universal unit — the metre.
Between five and six thousand years ago across Egypt, Mesopotamia, and the Indus valley, humans first began formally standardising units of measure. “Cubits” were one of the first to arise, defined as the distance between the elbow and tip of the middle finger (pretty obvious if you know the English word cubit derives from the Latin word for Elbow, “cubitum”, not so much for those who don’t). Cubits were then dissevered into spans, the width of a thumb-tip to little-finger-tip; palms, the width of a hand; and digits, the width of a middle finger, cleverly breaking down measurements into halves, sixths, and twenty-fourths. This is likely the origin of yards, feet, and inches, though the evidence for this is somewhat sparse. It’s also worth noting that similar units were used around the world. The Indian hasta is equivalent to a cubit and Chinese chi and Japanese shaku are similar to that of a span. The list can go on but it’s clear — the most convenient way to universally convey length was to use the human body.
This remained true for thousands of years, though the body parts did change somewhat. In 790, Charlemagne introduced a new unit of length called the toise (de l’Écritoire) which was established as the distance between the fingertips of a man with outstretched arms. Groundbreaking. Completely different from the Greek orguia and the English fathom. Though the toise, in one form or another, stuck around for a thousand years before it was eventually replaced by the metre. Broken down into six pieds (feet), 72 pouces (inches), or 864 lignes (lines), the toise was standardised as an iron bar built into a pillar of the Grand Châtelet in Paris. Though the date at which this occurred is unknown, we do know it was referenced in a 1394 survey and remained there all the way up until 1667 when the pillar warped the bar and distorted the standard, requiring a new one to be commissioned. They managed to make it 0.5% shorter than the old toise, causing many complaints, but they standardised it anyway and called it the “Toise du Chatelet”.
This highlighted the need to move away from physical bars and begin using well known natural processes, and in 1671 Jean Piccard did exactly that. He suggested that twice the length of a seconds pendulum, 440.5 lignes according to his measurements, should be a “toise universelle”. A great idea as the period of a simple pendulum is only related to its length and acceleration due to gravity. Though you may notice a slight issue with this; acceleration due to gravity is not a global constant, it fluctuates due to the shape of the Earth and random density variations, though this wasn’t known at the time. It was only revealed when the length of a seconds pendulum was measured in French Guiana and found to be 0.3% shorter than one in Paris. This opened up an important question which sparked fierce debate in the academic community — what was the shape of the Earth? Newton was adamant it was an oblate spheroid (slightly squashed at the poles), due to the centrifugal force at the equator being larger than that exerted at the poles. Though followers of Descartes believed it was shaped like a prolate spheroid (slightly squashed at the equator), due to his theory of vortices. It would take 50 years and the first large-scale international scientific expedition before the correct answer was known.
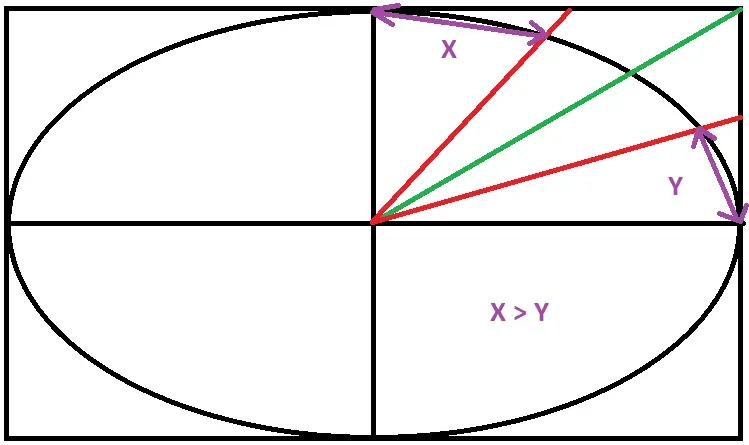
In 1735, deciding it was time to settle the debate on the shape of the Earth, King Louis XV and the French Academy of Sciences dispatched teams to the Equator and Arctic circle to determine which was larger; the equatorial circumference of Earth, or the polar circumference. Each team measured the linear distance of a degree of latitude using trigonometric surveying, finding that at the equator, one degree is 56,753 toises; whereas in the arctic circle, it is 57,437 toises. With this it becomes obvious Earth must be an oblate spheroid (I’ve drawn an astonishing diagram using paint, seen below), proving Newton correct and, when combined with longitudinal measurements, enables one to calculate the flattening of the Earth — the ratio between its semi-major and semi-minor axes. The flattening was calculated to be ~ 1/334 and the dataset used to define a new unit, the Toise of Peru. This name didn’t stick around for long though, as France officially adopted the unit in 1766 and renamed it the “Toise de l’Académie”.
If you draw the Earth as an ellipse in a box and dissect it, evenly splitting the sides of the box, you can see that nearer the poles, degrees of latitude become linearly longer than those at the equator. This diagram has enlarged the effect.
It wasn’t long before the French Revolution set the Toise aflame. Revolutionaries wanted to remove old traditions and so began implementing changes throughout society. The decimal system of time was implemented, dividing a day into 10 hours with 100 minutes per hour and 100 seconds per minute. This was thoroughly rejected, but decimal measurements of weight and length have been the standard ever since. France first adopted the metre as their standard unit of length in 1791. It was defined as one ten-millionth of the distance from the North pole to the equator along the meridian running through Paris. In pursuit of an accurate actualisation of this metre, astronomers Delambre and Méchain embarked on a seven year mission to measure the meridian arc connecting Dunkirk and Barcelona. Combining their precise knowledge of this distance with the Earth flattening previously measured, they could extrapolate their small, measured segment to a full ellipse and calculate the Earth’s polar circumference. Their result was 20,522,960 toises, equivalent to 39,999,249.04 modern day metres. You may notice this result is a little short of the actual polar circumference of the earth; 40,007,863 m by ~0.02%, and is mainly due to the Earth flattening factor propagating error within their calculation. The modern accepted value is close to 1/298, while they were working with 1/334. All this resulted in their measured metre, the one actually physically adopted, being 0.2mm shorter than their theoretically proposed metre.
Though not exactly the result they were aiming for, the metre was immortalised as a platinum bar and stored within the national Archives in June 1799. It served as the metre’s yardstick for the following 100 years becoming known as the mètre des Archives. The rest of Europe slowly adopted the metric system in academic circles with it eventually trickling down into everyday life. However, as geodesy became more accurate and reliable, the Earth flattening parameter was continuously revised, further demonstrating that the relationship between the actual metre and its theoretical definition was ill-defined. In 1867, the international prototype metre was proposed to quash these worries by simply defining a metre as the length of the bar in the archives “in the state in which it shall be found”. The Metre Convention was later held in 1875 to create a new metre bar which wasn’t a relic of the French Revolution. Over pure platinum a 90% platinum, 10% iridium X-shaped bar was created with etchings one metre apart (as defined by the old bar and seen in the first image). The alloy was harder than platinum alone and the X-shaped cross section was less prone to flexing during measurements. Thirty of these prototype bars were created and sent out to signatory nations of the Metre Convention with the official definition being stated as “prototype, at the temperature of melting ice, shall henceforth represent the metric unit of length”.
The metre was technically redefined in 1927, although it was really just an update to the instructions on how to measure the prototype bars. Other developments at the time were much more interesting. With the advent of interferometry, wavelengths of light produced by lamps of different gases could be precisely measured. The gas’ wavelength could then be utilised as a unit itself and used to measure the bars, defining the metre in terms of a truly reproducible natural phenomenon. Therefore at the same meeting, a secondary definition of the metre was stated as 1,553,164.13 cadmium wavelengths. It was thought this definition offered no additional precision over the prototype bar so unfortunately did not achieve primary status.
To increase the precision of interferometric measurements and therefore the metre, scientists went back to the lab and began analysing the qualities of different gases. Following advances in atomic physics and general experimental physics, cadmium was found to be suboptimal as the emission lines used to measure its wavelength were found to be a group of lines, reducing the precision of measurements. This was due to naturally sourced cadmium containing eight different isotopes, each of which emit at a slightly different frequency. To prevent this nonsense and obtain a more precise measurement krypton-86 was chosen as the new standard. Being a single isotope removes emission lines and it also has even-even nuclei, which means no pesky interaction between the nucleus and electrons producing even more emission lines. Moreover, it can be used to produce very sharp, well defined lines as krypton-86 can operate at low temperatures and contains heavy atoms, reducing the effect of doppler broadening. The metre was therefore redefined in 1960 to be equal to 1,650,763.73 krypton-86 wavelengths (in a vacuum obviously, with some stipulations on the exact transition which produces the emission line). This was finally the first official and practical definition based on reproducible natural phenomena!
In the same year as this new definition, the laser was invented. It was later used to show that the new krypton standard was ambiguous as the wavelength could be measured differently depending upon where you started on the emission line. Further advances in technology enabled high precision measurements of both the frequency and wavelength of laser light, essentially resulting in a measurement of the speed of light. It was found to travel at exactly 299,792,458 metres per second (once the ambiguity of the krypton line was settled by simply making a decision on where it should be measured from). With this, the metre was redefined in 1983 as the distance travelled by light in 1/299,792,458 of a second. Since then, the definition has been reworded once more and now specifically states the same relationship, though with the addendum of the second defined in terms of the caesium frequency. With these new definitions, the metre has become intrinsically linked to time and the universal constant of the speed of light. So next time someone asks you how long something is, be sure to reply in terms of speed of lights per caesium frequencies, I’m sure they’ll find it really helpful.